Question

Find b, given that a = 18.2, B = 62°, and C = 48°. Round answers to the nearest whole number. Do not use a decimal point or extra spaces in the answer or it will be marked incorrect.

Answer 1

17

Explanation:

We have been given that in triangle ABC, measure of angle B is 62 degrees and measure of angle C is 48 degrees. The length of side opposite to angle a is 18.2. We are asked to find length of side b.

We will use law of sines to solve for side b.

`\frac{a}{\text{sin}(A)}=\frac{b}{\text{sin}(B)}=\frac{c}{\text{sin}(C)}`

`m\angle A+m\angle B+m\angle C=180^(\circ)\\\\m\angle A+62^(\circ)+48^(\circ)=180^(\circ)`

`m\angle A+110^(\circ)=180^(\circ)`

`m\angle A+110^(\circ)-110^(\circ)=180^(\circ)-110^(\circ)`

`m\angle A=70^(\circ)`

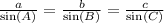
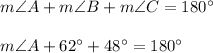
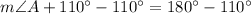
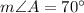
Upon substituting our given values, we will get:

`\frac{18.2}{\text{sin}(70^(\circ))}=\frac{b}{\text{sin}(62^(\circ))}`

`\frac{18.2}{\text{sin}(70^(\circ))}*\text{sin}(62^(\circ))=\frac{b}{\text{sin}(62^(\circ))}*\text{sin}(62^(\circ))`

`\frac{18.2}{\text{sin}(70^(\circ))}*\text{sin}(62^(\circ))=b`

`b=\frac{18.2}{\text{sin}(70^(\circ))}*\text{sin}(62^(\circ))`

`b=(18.2)/(0.939692620786)*0.882947592859`

`b=19.1551999*0.882947592859`

`b=16.9130376`

`b\approx 17`

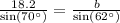
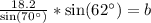
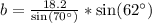
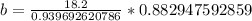
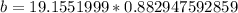
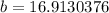
Therefore, the length of side b is 17 units.