Question

Two angles of a triangle measure 30° and 60°. Which of the following is true of the sides opposite these angles?

The side opposite the 30° angle is longer than the side opposite the 60° angle.

The side opposite the 60° angle is longer than the side opposite the 30° angle.

The sides opposite the 60° angle is twice as long as the side opposite the 30°

The sides opposite the 60° angle is twice as long as the side opposite the 30° angle.

There is no way to compare the sides opposite the angles.

Answer 1

The side opposite the 60° angle is longer than the side opposite the 30° angle.

Answer 2

Let

x-------> the side opposite the
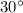`30\°` angle

y------> the side opposite the
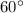`60\°` angle

we know that

If two angles of a triangle measure
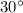`30\°` and
`60\°`

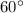
then

the third angle measure
`90\°`

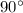
Is a right triangle

Remember that

`sin(30\°)=cos (60\°)=(1)/(2) \\\\sin(60\°)=cos(30\°)= (√(3))/(2) \\ \\tan(30\°)= (√(3))/(3)\\\\tan(60\°)=√(3)`

Statements

case A) The side opposite the
`30\°` angle is longer than the side opposite the
`60\°` angle

The statement is false

Because, the ratio of the side opposite the
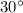`30\°` angle to the side opposite the
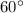`60\°` angle is equal to

`(x)/(y) =(1)/(√(3))`

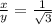
so

The side opposite the
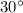`30\°` angle is smaller than the side opposite the
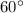`60\°` angle

case B) The side opposite the
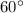`60\°` angle is longer than the side opposite the
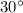`30\°` angle

The statement is true

Because, the ratio of the side opposite the
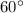`60\°` angle to the the side opposite the
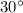`30\°` angle is equal to

`(y)/(x) =√(3)`

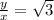
case C) The sides opposite the
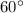`60\°` angle is twice as long as the side opposite the
`30\°`

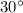
The statement is false

Because, the side opposite the
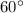`60\°` angle is equal to

`y=√(3)x`

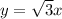
case D) There is no way to compare the sides opposite the angles

The statement is false

Because, we can use the trigonometric functions to be able to compare the ratio of the sides opposite the angles