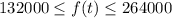Answer:
Step-by-step explanation:
The domain is
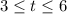 to represent the time values between 3 and 6 hours, including the endpoints. This represents the set of possible inputs to the function.
to represent the time values between 3 and 6 hours, including the endpoints. This represents the set of possible inputs to the function.
The function f(t) = 44000t is an increasing function. This means the smallest range value corresponds to the smallest domain value.
Plug in t = 3 to find that:
f(t) = 44000t
f(3) = 44000*3
f(3) = 132000
This says he mows 132,000 sq ft of lawn in 3 hours.
Now plug in the largest domain value to find the largest range value
f(t) = 44000t
f(6) = 44000*6
f(6) = 264000
He mows 264,000 sq ft of lawn in 6 hours.
The range is the set of f(t) values between 132,000 and 264,000
We can write that as