Question

Select the correct answer. What is the solution to the equation? (x - 2)^1/2 + 4 = x A. -3 and -6 B. 3 and 6 C. -3 D. 6

Answer 1

The answer is D. 6

Explanation:

Add both sides:

(x - 2)^1/2 + 4 + (-4) = x + (-4)

(x - 2)^1/2 = -4

Solve exponent:

(x - 2)^1/2 = x - 4

((x - 2)^1/2)^2 = (x - 4)^2

x − 2 = x^2 − 8x + 16

x − 2 − (x^2 − 8x + 16) = x^2 − 8x + 16 − (x^2 − 8x + 16)

−x^2 + 9x − 18 = 0

(−x + 3)(x − 6) = 0

−x + 3 = 0 or x − 6 = 0

x = 3 or x = 6

Check the answers: (Plug them in to see what will work.)

x = 3 (won't work)

x = 6 (does work)

Therefore,

x = 6

Answer 2

D. x = 6

Explanation:

Given equation:

`(x-2)^{(1)/(2)}+4=x`

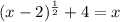
Subtract 4 from both sides:

`\implies (x-2)^{(1)/(2)}+4-4=x-4`

`\implies (x-2)^{(1)/(2)}=x-4`

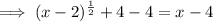
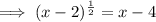
Square both sides:

`\implies \left( (x-2)^{(1)/(2)}\right)^2=(x-4)^2`

`\implies x-2=(x-4)^2`

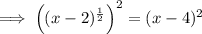
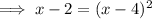
Expand the brackets on the right side:

`\implies x-2=(x-4)(x-4)`

`\implies x-2=x^2-8x+16`

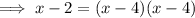
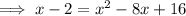
Subtract x from both sides:

`\implies x-2-x=x^2-8x+16-x`

`\implies -2=x^2-9x+16`

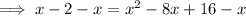
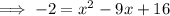
Add 2 to both sides:

`\implies -2+2=x^2-9x+16+2`

`\implies 0=x^2-9x+18`

`\implies x^2-9x+18=0`

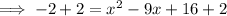
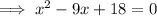
Factor the left side of the equation:

`\implies x^2-6x-3x+18=0`

`\implies x(x-6)-3(x-6)=0`

`\implies (x-3)(x-6)=0`

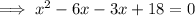
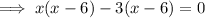
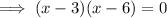
Apply the zero-product property:

`\implies x-3=0 \implies x=3`

`\implies x-6=0\implies x=6`

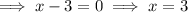
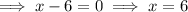
Therefore, the solutions of the quadratic equation are:

`x=3, \quad x=6`

Input both solutions into the original equation to check their validity:

`\begin{aligned}x=3 \implies (3-2)^{(1)/(2)}+4&=3\\(1)^{(1)/(2)}+4&=3\\1+4&=3\\5&=3\end{aligned}`

`\begin{aligned}x=6 \implies (6-2)^{(1)/(2)}+4&=6\\(4)^{(1)/(2)}+4&=6\\2+4&=6\\6&=6\end{aligned}`

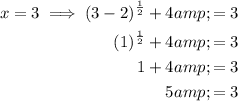
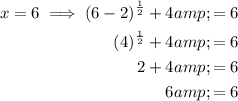
Therefore, the only valid solution to the given equation is x = 6.