Question

Don't answer if you don't know the answer.

find the indefinite integral


`\int\limits { (x+2)/(x^2+1) } \, dx`

Answer 1

`\displaystyle \int {(x + 2)/(x^2 + 1)} \, dx = 2arctan(x) + (ln|x^2 + 1|)/(2) + C`

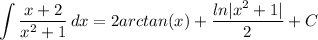
General Formulas and Concepts:

Algebra I

• Terms/Coefficients
• Expanding

Calculus

Differentiation

• Derivatives
• Derivative Notation

Derivative Property [Addition/Subtraction]:
`\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]`

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Integration

• Integrals
• [Indefinite Integrals] Integration Constant C

Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

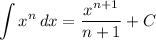
Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

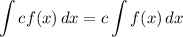
Integration Property [Addition/Subtraction]:
`\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx`

U-Substitution

Explanation:

Step 1: Define

Identify

`\displaystyle \int {(x + 2)/(x^2 + 1)} \, dx`

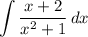
Step 2: Integrate Pt. 1

Set variables for u-substitution.

1. Set u:
   `\displaystyle u = x^2 + 1`
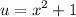
2. [u] Differentiate [Basic Power Rule, Addition/Subtraction]:
   `\displaystyle du = 2x \ dx`

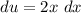
Step 3: Integrate Pt. 2

1. [Integral] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle \int {(x + 2)/(x^2 + 1)} \, dx = (1)/(2)\int {(2(x + 2))/(x^2 + 1)} \, dx`
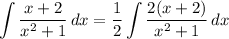
2. [Integrand] Expand:
   `\displaystyle \int {(x + 2)/(x^2 + 1)} \, dx = (1)/(2)\int {(2x + 4)/(x^2 + 1)} \, dx`
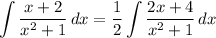
3. [Integral] Rewrite [Integration Property - Addition/Subtraction]:
   `\displaystyle \int {(x + 2)/(x^2 + 1)} \, dx = (1)/(2) \bigg[ \int {(2x)/(x^2 + 1)} \, dx + \int {(4)/(x^2 + 1)} \, dx \bigg]`
4. [2nd Integral] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle \int {(x + 2)/(x^2 + 1)} \, dx = (1)/(2) \bigg[ \int {(2x)/(x^2 + 1)} \, dx + 4\int {(1)/(x^2 + 1)} \, dx \bigg]`
5. [1st Integral] U-Substitution:
   `\displaystyle \int {(x + 2)/(x^2 + 1)} \, dx = (1)/(2) \bigg[ \int {(1)/(u)} \, du + 4\int {(1)/(x^2 + 1)} \, dx \bigg]`
6. [1st Integral] Logarithmic Integration:
   `\displaystyle \int {(x + 2)/(x^2 + 1)} \, dx = (1)/(2) \bigg[ ln|u| + 4\int {(1)/(x^2 + 1)} \, dx \bigg]`
7. [Integral] Arctrig Integration:
   `\displaystyle \int {(x + 2)/(x^2 + 1)} \, dx = (1)/(2) \bigg[ ln|u| + 4 \bigg( (1)/(1)arctan \Big( (x)/(1) \Big) \bigg) \bigg] + C`
8. Simplify:
   `\displaystyle \int {(x + 2)/(x^2 + 1)} \, dx = (1)/(2) \bigg[ ln|u| + 4arctan(x) \bigg] + C`
9. Expand:
   `\displaystyle \int {(x + 2)/(x^2 + 1)} \, dx = 2arctan(x) + (ln|u|)/(2) + C`
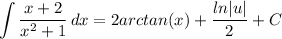
10. Back-Substitute:
    `\displaystyle \int {(x + 2)/(x^2 + 1)} \, dx = 2arctan(x) + (ln|x^2 + 1|)/(2) + C`

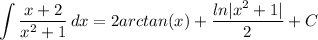
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration