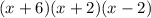Question

Factor completely. x 3 + 6x 2 - 4x - 24

a.(x + 6)(x - 2)(x + 2)
b.(x + 2)(x - 6)(x + 2)
c.(x - 6)(x + 2)(x + 2)x^3 + 6x^2 - 4x - 24 = x^2(x + 6) - 4(x + 6) = (x + 6)(x^2 - 4) = (x + 6)(x + 2)(x - 2)

Answer 1

I really suck at explaining with words so here a photo, I hope you understand
A

Answer 2

Option (a) is correct.

The factored form of given expression
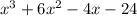`x^3+6x^2-4x-24` is
`(x+6)(x+2)(x-2)`

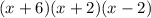
Explanation:

Given expression
`x^3+6x^2-4x-24`

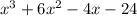
We have to factorize the given expression completely.

Consider the given expression
`x^3+6x^2-4x-24`

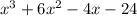
We will solve the given expression by grouping terms and taking common factor common.

`x^3+6x^2-4x-24`

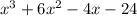
Taking
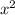`x^2` common from first two terms and -4 common from last two terms, we have,

`x^2(x+6)-4(x+6)`

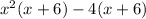
Taking (x+6) common , we have,

`x^2(x+6)-4(x+6)=(x+6)(x^2-4)`

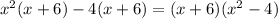
Also , using algebraic identity
`a^2-b^2=(a+b)(a-b)`

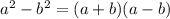
We have a = x , b = 2

We have,

`x^2(x+6)-4(x+6)=(x+6)(x^2-4)`

`\Rightarrow (x+6)(x^2-4)=(x+6)(x+2)(x-2)`

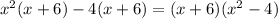
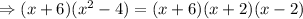
Thus, the factored form of given expression
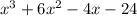`x^3+6x^2-4x-24` is
`(x+6)(x+2)(x-2)`