Question

In two or more complete sentences, compare the number of x-intercepts in the graph of f(x) = x2 to the number of x-intercepts in the graph of g(x) = (x-2)2 -3. Be sure to include the transformations that occurred between the parent function f(x) and its image g(x).

Answer 1

2 left on the x axis 7 up on the y axis

Explanation:

Answer 2

The number of y-intercept of g(x) is greater than y-intercept of f(x).

Explanation:

The given functions are

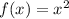`f(x)=x^2` (parent function)

`g(x)=(x-2)^2-3`

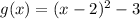
These are parabolic functions.

The standard form of parabolic functions is

`f(x)=a(x-h)^2+k`

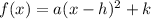
Where, a is scale factor and (h,k) is vertex of parabola.

If h>0, then graph of parent function shifts h units right and If h<0, then graph of parent function shifts h units left.

If k>0, then graph of parent function shifts k units upward and If k<0, then graph of parent function shifts k units downward.

Therefore the graph of f(x) shifts 2 units right and 3 units downward to get graph of g(x).

Using the standard form we can say that f(x) has vertex (0,0) and g(x) has vertex (2,-3).

SInce value a>0, therefore f(x) an g(x) are upward parabola.

Since the vertex of f(x) is origin, therefore f(x) has one y-intercept, i.e., (0,0).

Since the vertex of g(x) is (2,-3) and it is an upward parabola, therefore g(x) has two y-intercepts.

`0=(x-2)^2-3`

`x=0.268,3.732`.

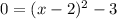
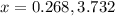Therefore number of y-intercept of g(x) is greater than y-intercept of f(x).