Question

Your school wants to have 5 computers for every 12 students. There are now 125 computers and 924 students. How many more computers are needed to have a ratio of 5 to 12?

Answer 1

260 computers will be required more for 125 students.

Explanation:

As it is given in the question school wants to have 5 computer for every 12 students.

Current number of computers are 125 and number of students are 924.

Let the number of computers is n for 924 students and the ratio of computers and students is 5 : 12

So
`\frac{\text{Current number of computers}}{\text{Current number of students}}`=
`(5)/(12)`

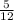
Therefore,
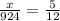
`(x)/(924)=(5)/(12)`

x =
`(924* 5)/(12)=385`

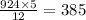
But the number computers is = 125

Therefore, number of computers required more will be

385 - 125 = 260

260 computers will be required more for 125 students.

Answer 2

You can first set up a ratio to see how many TOTAL computers are needed for a r to 12 ratio.
(5/12) = (x/924) Now cross multiply to solve. 12x = 5(924) 12x = 4620
Divide both sides by 12. x = 385
There are a total of 385 computers needed for the school to have a 5:12 ratio.
Since the school already has 125 computers subtract 385-125 = 260. They need to purchase 260 more computers.