Answer:
The recursive formulas for the following sequence is
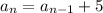 .
.
Explanation:
The given explicit formula is
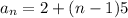
Find the (n-1)th term of the sequence.
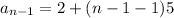
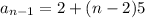 .... (1)
.... (1)
The given explicit formula can be written as

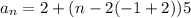
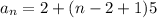
Use distributive property.
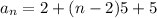
Using equation (1), we get
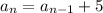
Therefore the recursive formulas for the following sequence is
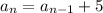 .
.