Question

If sinx is approximately 0.2588, what is the measurement of x to the nearest degree? Approximately, what is the cosine of the angle that is complementary to x?

Answer 1

Part 1)
`x=15\°`

Part 2)
`cos(75\°)=0.2588`

Explanation:

Part 1) we have

`sin(x)=0.2588`

using a calculator

`x=sin^(-1)(0.2588)=15\°`

Part 2)

we know that

If two angles are complementary

`\alpha+\beta=90\°` ------> complementary angles

then

`cos(\alpha)=sin(\beta)`

In this problem

we have

`x=15\°`

The angle complementary to x is equal to

`90\°-15\°=75\°`

so

`cos(75\°)=sin(15\°)`

therefore

`cos(75\°)=0.2588`

Answer 2

The value of x is 15°,

The cosine of the angle that is complementary to x is 0.2588(approx)

Explanation:

Given,

`sin x = 0.2588`

`\implies x = sin^(-1)(0.2588)= 14.9988703055\approx 15^(\circ)`

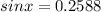
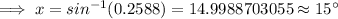
Hence, the value of x is 15°,

Now, the complementary angles are the two angles who give the sum of 90°,

⇒ Complementary angle of x = 90° - x = 90° - 15° = 75°

Thus, the cosine of the angle that is complementary to x,

cos(90-x) = cos 75° = 0.2588190451 ≈ 0.2588