Step-by-step explanation:
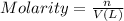
n = moles of compound
V =Volume of the solution in Liters
Moles of potassium sulfate ,n=

Volume of the solution = 1.50 L
Molarity of the solution =
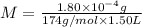
Molarity of potassium sulfate solution:
![[K_2SO_4]=M=6.8965* 10^(-7) mol/L](https://img.qammunity.org/2018/formulas/chemistry/college/swar6t3o2gulinl2ypooze119pz4l8hvbz.png)
1 mole of potassium sulfate gives 2 moles of potassium ions and 1 mole of sulfate ions.
Molarity of potassium ions in the solution:
![[K^+]=2* M=2* 6.8965* 10^(-7) mol/L=1.3793* 10^(-6) mol/L](https://img.qammunity.org/2018/formulas/chemistry/college/ifvez8tk4vltn4oiga3ov6nf1sxqrihooa.png)
Molarity of sulfate ions in the solution:
![[SO_4^(2-)]=1* 6.8965* 10^(-7) mol/L=6.8965* 10^(-7) mol/L](https://img.qammunity.org/2018/formulas/chemistry/college/umcelktx5nbsh2a6mu9leobrncdrxzunsy.png)
Concentration in ppm:
ppm = Milligram of compo present in 1 liter solution.
ppm = Molarity × Molar mass of compound × 1000
Concentration of potassium ion in ppm:
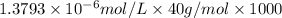
![[K^+]=0.05517 ppm](https://img.qammunity.org/2018/formulas/chemistry/college/xc3h9bhkv0jjhfc6r2zrbft36geq98j0no.png)
Concentration of sulfate ions in ppm:

![[SO_4^(2-)]=0.06620 ppm](https://img.qammunity.org/2018/formulas/chemistry/college/usg506a9lbgey77vowsd8ipvdn89fwmnst.png)