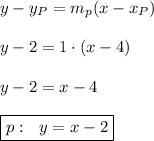Question

Write an equation of the perpendicular bisector of the segment with end points M(1,5) and N(7,-1)

Answer 1

The perpendicular bisector of the segment passes through the midpoint of this segment. Thus, we will initially find the midpoint P:


`P=((1,5)+(7,-1))/(2)=((8,4))/(2)=(4,2)`

Now, we will calculate the slope of the segment support line (r). After this, we will use the fact that the perpendicular bisector (p) is perpendicular to r:


`m_r=(\Delta y)/(\Delta x)=(5-(-1))/(1-7)=(6)/(-6)\iff m_r=-1`



`p\perp r\Longrightarrow m_p\cdot m_r=-1\Longrightarrow m_p\cdot(-1)=-1\iff m_p=1`

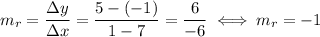
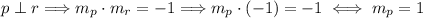
We can calculate the equation of p by using its slope and its point P:


`y-y_P=m_p(x-x_P)\\\\ y-2=1\cdot(x-4)\\\\ y-2=x-4\\\\ \boxed{p:~~y=x-2}`