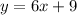Question

A given line has the equation 2x+12y=-1.

What is the equation in slope intercept form, of the line that is perpendicular to the given line and passes through the point (0,9)?
y=(____)x+9

Answer 1

`y = 6x+9`

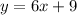
Explanation:

Point slope form:

The equation of line passes through the point
`(x_1, y_1)` is given by:

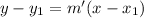`y-y_1=m'(x-x_1)` ....[1]

where, m' is the slope

As per the statement:

A given line has the equation

2x+12y=-1

Subtract 2x from both sides we have;

`12y =-2x-1`

Divide both sides by 12 we have;

`y = -(1)/(6)x-(1)/(12)`

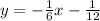
On comparing with slope intercept form equation y=mx+b we get;

`m= -(1)/(6)`

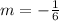
We have to find the equation in slope intercept form, of the line that is perpendicular to the given line and passes through the point (0,9)

Since, a line is perpendicular to a given line.

⇒
`m * m' =-1`

⇒
`m'= (-1)/(m)`

⇒
`m' = (-1)/((-1)/(6))`

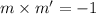
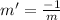
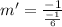
Simplify:

m' = 6

Substitute the value of m' and (0, 9) in [1] we have;

`y-9 =6(x-0)`

⇒
`y-9 = 6x`

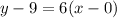
Add 9 to both sides we have;

`y = 6x+9`

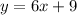
Therefore, the equation in slope intercept form, of the line that is perpendicular to the given line and passes through the point (0,9) is,
`y = 6x+9`

Answer 2

2x+12y=-1
y = -1x/6 -1/12

Perpendicular lines are lines that cross one another at a 90° angle. They have slopes that are opposite reciprocals of one another. Therefore, the slope of the perpendicular line in this problem is the opposite reciprocal of -1/6 which is 6. The equation would be

y=(6)x+9