Question

Tom throws a ball into the air. The ball travels on a parabolic path represented by the equation h = -8t 2 + 40t, where h represents the height of the ball above the ground and t represents the time in seconds. How many seconds does it take the ball to reach its highest point? What ordered pair represents the highest point that the ball reaches as it travels through the air?

Answer 1

it traveled 160ft in the air

Answer 2

2.5 seconds , (50,2.5)

Explanation:

Here we are given the equation of the path as

`h=-8t^2+40t`

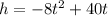
taking -8 out as GCF

`h=-8(t^2-5t)`

adding and subtracting
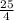`(25)/(4)` in the bracket

`h=-8(t^2-5t+[tex]-(25)/(4))`

`h=-8(t^2-5t+((5)/(2))^2)+8*(25)/(4)`

`h=-8(t-(5)/(2))^2+50`

`(h-50)=-8(t-(5)/(2))^2`

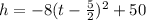
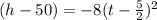
Hence if we compare it with the standard equation of a parabola

we get that

vertex of the parabola formed above is

`(50,(5)/(2))`

Where h is on y axis and t is on x axis.

Hence the throw attains maximum height at t = 2.5 sec

and the coordinates of the maximum height attained will be (50,2.5)