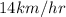Answer:
(A) Northbound bicyclist=20 km/hr, southbound bicyclist=14 km/h.
Explanation:
The total time taken is= 1 hour 15 min=1.25 hours. Let the distance traveled by bicyclist heading in the south direction is represented by
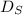 and the distance traveled by the bicyclist heading in north direction be
and the distance traveled by the bicyclist heading in north direction be
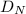 , then according to question
, then according to question
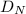 +
+
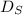 =42.5km. (1)
=42.5km. (1)
Therefore, using speed=
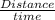 ,
,
Distance traveled by bicyclist heading in the south direction is
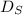 = speed × time= 1.25×S, where S is the speed of the bicyclist heading in south........(2)
= speed × time= 1.25×S, where S is the speed of the bicyclist heading in south........(2)
Since, The bicyclist heading in north direction is 6km/hr faster than the bicyclist heading in south direction, therefore,
Speed of bicyclist heading in north direction will be, N=S+6...........(3)
Let the distance travelled by the bicyclist heading in north direction is represented as
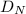 .
.
Therefore,
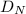 = 1.25N
= 1.25N
=1.25(S+6)
=1.25S+ 7.5 (4)
Now, subtracting (2) from (4), we have
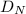 -
-
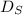 =1.25S+7.5-1.25S
=1.25S+7.5-1.25S
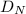 -
-
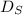 =7.5 (5)
=7.5 (5)
Now, from equation (1), we have
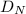 +
+
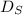 =42.5, solving equation (1) and equation (5), we get
=42.5, solving equation (1) and equation (5), we get
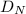 =25km.
=25km.
Now, substituting this value of
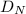 in equation (1),
in equation (1),
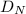 +
+
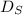 =42.5
=42.5
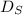 =42.5-25.0
=42.5-25.0
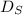 =17.5km
=17.5km
Now,speed of the bicyclist heading in north direction will be:
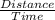
=
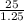
=
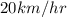
Also, Speed of bicyclist heading in south direction=
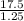
=