Question

Please help! I am having a total mind blank right now.

Write a coordinate proof for the following theorem. If a quadrilateral is a kite then it's diagonals are perpendicular.

Answer 1

I'll try my best to help you :)
You would compute the slopes of the diagonals WY and ZX
The slopes of the perpendicular lines have a product of -1
Now see if the slopes you get multiply to -1
If they do, the diagonals are perpendicular
I'm sorry if this doesn't help

Answer 2

Theorem: If a quadrilateral is a kite then it's diagonals are perpendicular.

Proof:- In kite WXYZ, let O(a,b) be the intersection point of the diagonals .

Also the distance formula is given by ,

Distance from
`(x_1,y_2)\ and\ (x_2,y_2)=√((x_2-x_1)^2-(y_2-y_1)^2)`

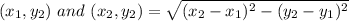
In ΔWOX,

OX=a [since the coordinate of x changes but not y, thus the distance from O to X=a]

WO= 3b [since the coordinate of y changes but not x, thus the distance from O to W = 4b-b=3b]

WX=
`√((2a-a)^2+(4b-b))=√(a^2+9b^2)`

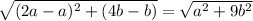
We can see that

`WX^2=a^2+9b^2=OX^2+WO^2\\\Rightarrow\ WX^2=OX^2+WO^2`

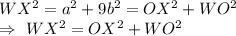
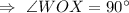`\\\Rightarrow\ \angle{WOX}=90^(\circ)` [By the converse of Pythagoras theorem]

⇒ The diagonals are perpendicular.

Hence proved.