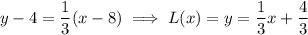Question

Find the tangent line approximation, L(x), of x^2/3  at x = 8.

Answer 1

When
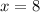
`x=8`, the function
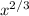
`x^(2/3)` takes on a value of
`8^(2/3)=\sqrt[3]{64}=4`. So you're looking to find the tangent line to
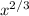
`x^(2/3)` through the point
`(8,4)`.

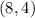
The tangent line through this point has the value of the derivative of
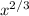
`x^(2/3)` when
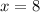
`x=8`. The derivative is, by the power rule,


`(\mathrm d)/(\mathrm dx)x^(2/3)=\frac23 x^(-1/3)\stackrel{x=8}\implies\text{slope}=\frac23*8^(-1/3)=\frac13`

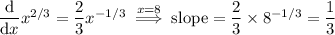
The point-slope form of the tangent line is


`y-4=\frac13(x-8)\implies L(x)=y=\frac13x+\frac43`