Answer:
q = -1
Explanation:
We are given the inequality
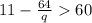
We want to find out which value of q is a solution to the inequality. In other words, which value of q makes the statement true?
We can substitute the values given for q into the inequality to see this.
Let's start with q=2.
Replace q with 2.
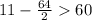
Divide 64 by 2.
64/2= 32
11 - 32 > 60
Subtract 32 from 60
11-32 = -21
-21 > 60
The inequality reads "-21 is greater than 60", which is false (negative numbers are less than positive ones).
This means q=2 is NOT an answer.
Next, let's try q=-2
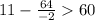
64/-2 = -32
11 - - 32 > 60
- - 32 means subtracting a negative, which is the same as adding 32 to 11.
11 + 32 > 60
43 > 60
This is also NOT true (it reads "43 is greater than 60").
So q=-2 is also NOT an answer.
Now, let's try q = -1
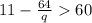
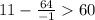
64/-1=-64
11 - -64 > 60
11 + 64 > 60
75 > 60
This reads "75 is greater than 60".
This is a true statement, meaning q = -1 IS an answer.
We are technically done, but just to be sure, we can check q=1 as well.
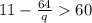
11 - 64 > 60
-53 > 60
This reads "-53 is greater than 60", which is false.
So this confirms that q = -1 is the only option that is an answer.