Final answer:
To find the equation of a parabola with vertex (0,0) and directrix y = -6, use the distance formula to equate the distance from a point on the parabola to the focus and to the directrix, which results in the parabolic equation y = (1/24)x^2.
Step-by-step explanation:
To write the equation of a parabola with vertex (0,0) and directrix y = -6, we can use the definition of a parabola: the set of all points that are equidistant from the directrix and the focus. In this case, since the vertex is at the origin and the directrix is a horizontal line below the x-axis, the focus must be at (0, 6). The distance formula for a point (x, y) to be on this parabola is the distance from (x, y) to the focus equals the distance from (x, y) to the directrix.
This gives us the equation:
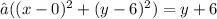
Squaring both sides, we get:

Simplifying this, we get:
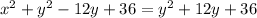
Subtracting y^2 and 36 from both sides yields:
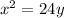
Dividing both sides by 24, we end up with the equation of the parabola:
