Question

Determine which of the lines are parallel and which of the lines are perpendicular. Select all of the statements that are true.

Line a passes through (-1, -17) and (3, 11).
Line b passes through (0,4) and (7,-5).
Line c passes through (7, 1) and (0, 2).
Line d passes through (-1,-6) and (1, 8).

Answer 1

Answers:

Line A is parallel to line D.

Line A is perpendicular to line C.

Line C is perpendicular to line D.

=====================================================

Step-by-step explanation:

Let's use the slope formula to calculate the slope of the line through (-1,-17) and (3,11)

`(x_1,y_1) = (-1,-17) \text{ and } (x_2,y_2) = (3,11)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (11 - (-17))/(3 - (-1))\\\\m = (11 + 17)/(3 + 1)\\\\m = (28)/(4)\\\\m = 7\\\\`

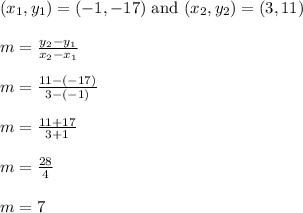
The slope of line A is 7

-------------

Now let's find the slope of line B.

`(x_1,y_1) = (0,4) \text{ and } (x_2,y_2) = (7,-5)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (-5 - 4)/(7 - 0)\\\\m = -(9)/(7)\\\\`

-------------

Now onto line C.

`(x_1,y_1) = (7,1) \text{ and } (x_2,y_2) = (0,2)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (2 - 1)/(0 - 7)\\\\m = (1)/(-7)\\\\m = -(1)/(7)\\\\`

-------------

Lastly we have line D.

`(x_1,y_1) = (-1,-6) \text{ and } (x_2,y_2) = (1,8)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (8 - (-6))/(1 - (-1))\\\\m = (8 + 6)/(1 + 1)\\\\m = (14)/(2)\\\\m = 7\\\\`

------------------------------

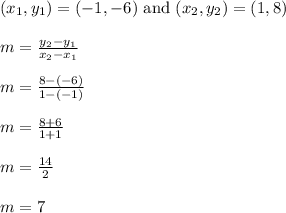
Here's a summary of the slopes we found

`\begin{array}c \cline{1-2}\text{Line} & \text{Slope}\\\cline{1-2}\text{A} & 7\\\cline{1-2}\text{B} & -9/7\\\cline{1-2}\text{C} & -1/7\\\cline{1-2}\text{D} & 7\\\cline{1-2}\end{array}`

Recall that parallel lines have equal slopes, but different y intercepts. This fact makes Line A parallel to line D.

Lines A and C are perpendicular to one another, because the slopes 7 and -1/7 multiply to -1. In other words, -1/7 is the negative reciprocal of 7, and vice versa. These two lines form a 90 degree angle.

Lines C and D are perpendicular for the same reasoning as the previous paragraph.

Line B unfortunately is neither parallel nor perpendicular to any of the other lines mentioned.

You can use a graphing tool like Desmos or GeoGebra to verify these answers.