Question

The decomposition of potassium chlorate yields oxygen gas. If the yield is 85%, how many grams of KClO3 are needed to produce 15.0 L of O2 ?

2KClO3(s) -- > 2KCl(s) + 3 O2(g)

Answer 1

2KClO3 = 2KCl + 3O2.

10 L are 10/22.4 moles as 1 mole of gas at STP occupies 22.4 L so 0.446 moles but you only get 95% yield so you need to make more than 0.446 moles -- you need 0.446/0.95 = 0.470 moles.

Two moles KClO3 give 3 moles O2 so you need 0.470*(2/3) moles KClO3 = 0.313 moles KClO3 and that has molar mass = 39 + 35.5 + 3*16 = 122.5 g so in g 0.313*122.5 = 38.4 g KClO3

Answer 2

`m_(KClO_3)=64.4gKClO_3`

Step-by-step explanation:

Hello,

At first, the undergoing chemical reaction is:

`2KClO_3(s)-->2KCl(s)+3O_2(s)`

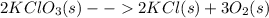
As 15.0 L of oxygen were produced, one computes this amount in moles considering STP conditions (0°C and 1 atm) for the ideal gas equation as shown below:

`n_(O_2)=(PV)/(RT) =(1atm*15.0L)/(0.082 (atm*L)/(mol*K) *273.15K)=0.670molO_2`

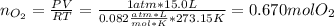
Now, since those moles are the actual obtained moles, one computes the theoretical moles of oxygen which are more precisely associated with the needed grams of potassium chlorate as follows:

`n_(O_2)^(Theoretical)=(0.670molO_2)/(0.85) =0.788molO_2`

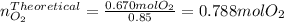
Finally, we apply the stoichiometry to determine the moles of potassium chlorate as shown below:

`m_(KClO_3)=0.788molO_2*(2molKClO_3)/(3molO_2) *(122.55gKClO_3)/(1molKClO_3) \\m_(KClO_3)=64.4gKClO_3`

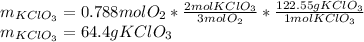
Best regards.