Question

A is in the shape of a quarter circle of radius 15 cm.

B is in the shape of a circle.
A
15 cm
The area of A is 9 times the area of B.
Work out the radius of B.
B

Answer 1

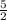`(5)/(2)` or 2.5cm

Explanation:

Hello! Let's help you with your question here!

Let's start by working out what we know and what we need. So, we know that P is a circle and Q is the shape of a quarter circle with a radius of 20cm. The area of Q is 9 times the area of P and we must find the radius of P.

To start, we're looking for area, so we should at least start looking at the area of a circle, given radius, which is:

`A=\pi r^2`

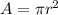
Now, we don't necessarily know r (radius) and the area either. However, we can try to use the quarter circle as our guide for the full circle. So, we want to find the area of the quarter circle, we can do that by using this formula!

`A=(1)/(4) \pi r^2`

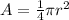
The reason why we put a
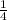`(1)/(4)` at the front of
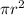`\pi r^(2)` is because we're only solving for a quarter of a circle instead of the entire circle.

Now that we have our formula! We can calculate the area of the quarter circle as follows:

`A=(1)/(4)\pi 15^2`

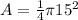
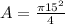`A=(\pi 15^2)/(4)` -We combine the fraction
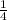`(1)/(4)` into the rest of the equation.

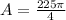`A=(225\pi )/(4)` - Evaluating
`15^2`

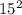
Now that we have the area of the quarter circle, we can now work on the full circle. What we know is that the area of A is 9 times of B, since we're finding the radius of B, we can essentially plug in the area and solve for the radius of the full circle. That would be as such:

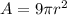`A=9\pi r^2` -We're using the area of circle A to find the radius of B.

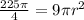`(225\pi )/(4) =9\pi r^2` - Plugging in the area of the quarter circle.

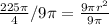`(225\pi )/(4)/9\pi =(9\pi r^2)/(9\pi )` - We divide
`9\pi` to get rid of it on the right side.

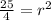`(25)/(4) =r^2` - When dividing by
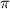`\pi`, the numerator
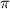`\pi` gets cancelled out.

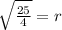`\sqrt{(25)/(4) }=r` -We square root to get rid of the squared.

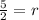`(5)/(2)=r` - Square rooted both numerator and denominator.

And there we have it! We finally get a radius of
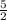`(5)/(2)` or 2.5cm.