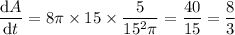Question

A spherical balloon is being inflated at the rate of 20 cubic feet per minute. at the instant when the radius is 15 feet, at what rate is the surface area increasing?

Answer 1

The surface area of the balloon is
`A=4\pi r^2`.

Differentiate both sides with respect to an arbitrary variable representing time:

`(\mathrm dA)/(\mathrm dt)=8\pi r(\mathrm dr)/(\mathrm dt)`

Meanwhile, the volume of the balloon is
`V=\frac43\pi r^3`.

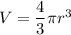
Differentiating with respect to
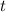
`t` yields

`(\mathrm dV)/(\mathrm dt)=4\pi r^2(\mathrm dr)/(\mathrm dt)`

You're told that, at the point when the radius
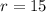
`r=15`, the volume of the balloon increases at a rate of
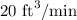
`20\text{ ft}^3/\text{min}`, which means
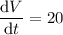
`(\mathrm dV)/(\mathrm dt)=20`. Use this to solve for the rate of change of the radius,
`(\mathrm dr)/(\mathrm dt)`.


`20=4\pi *15^2(\mathrm dr)/(\mathrm dt)\implies(\mathrm dr)/(\mathrm dt)=\frac5{15^2\pi}`

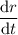
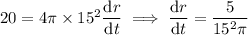
Substitute this into the equation for the rate of change of the surface area and solve for
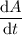
`(\mathrm dA)/(\mathrm dt)`.


`(\mathrm dA)/(\mathrm dt)=8\pi *15*\frac5{15^2\pi}=(40)/(15)=\frac83`