Question

The area of a rectangular room is 750 square feet. the width of the room is 5 feet less than the length of the room. which equations can be used to solve for y, the length of the room?

Answer 1

I hope this helps you

Answer 2

Width=25 ft and length=30 ft

Explanation:

In order to find the answer let's remember that the area (A) of a rectangle is:

`A=width*length`

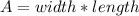
Let's assume that the length of the room is 'X' feet.

Becuase the problem mentioned that the width (Y) of the room is 5 feet less than the length, then:

`Y=X-5`

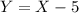
Now, using the area equation we have:

A=width*length

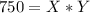`750=X*Y` but using the width expression we have:

`750=X*(X-5)`

`0=X^2-5X-750`

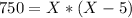
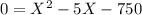
Using the root's equation we have:

`X=\frac{-b\±\sqrt{b^(2)-4ac}}{2a}`

`X=\frac{-(-5)\±\sqrt{(-5)^(2)-(4*1*(-750)}}{2*1}`

`X1=30`

`X1=-25`

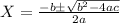
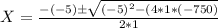
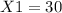
Because the length (X) can't be negative, then length=30 feet. In order to find the width we have:

`Y=X-5`

`Y=30-5`

`Y=25`

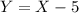
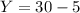
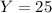
So the width is 25 feet.

In conclusion the room has a width=25 ft and length=30 ft.