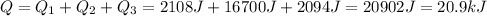Question

Heat of Fusion How much thermal energy is needed change 50.0 g of ice at -20.0°C to water at 10.0°C?

Answer 1

We should divide the problem into 3 separate processes.

1) Bring the temperature of the ice from
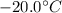
`-20.0^(\circ)C` to its melting point (
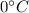
`0^(\circ)C`): the amount of heat needed in this process is

`Q_1=mC_s \Delta T`
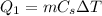
where

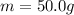
`m=50.0 g` is the mass of the ice

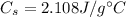
`C_s = 2.108 J/g^(\circ)C` is the specific heat capacity of ice

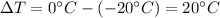
`\Delta T=0^(\circ)C-(-20^(\circ)C)=20^(\circ)C` is the increase of temperature

Plugging numbers into the equation, we find

`Q_1 = (50.0 g)(2.108 J/g^(\circ)C)(20^(\circ)C)=2108 J`

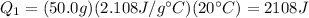
2) Fusion of ice
When the ice is at melting point, we need to add a certain amount of heat in order to melt it, and this amount of it is given by:

`Q_2 = mL_f`
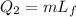
where

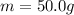
`m=50.0 g` is the mass of ice

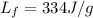
`L_f = 334 J/g` is the latent heat of fusion of ice

Plugging numbers into the equation, we find

`Q_2 = mL_f = (50.0g)(334 J/g)=16700 J`
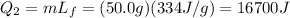
During this phase transition, the temperature of the ice/water does not change.

3) Bring the temperature of the water from
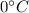
`0^(\circ)C` to
`10^(\circ)C`

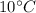
The amount of heat needed for this process is

`Q_3 = mC_s \Delta T`
where

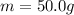
`m=50.0 g` is the mass of water

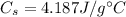
`C_s = 4.187 J/g^(\circ)C` is the specific heat capacity of water

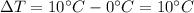
`\Delta T=10^(\circ)C-0^(\circ)C=10^(\circ)C` is the increase of temperature

Plugging numbers into the equation, we find

`Q_3 = (50.0 g)(4.187 J/g^(\circ)C)(10.0^(\circ)C)=2094 J`


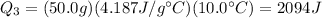
--> therefore, the total energy needed for the whole process is:

`Q=Q_1+Q_2+Q_3=2108 J+16700 J+2094 J=20902 J=20.9 kJ`