Answer:
RS : ST = 2 : 3
Explanation:
Coordinates of the endpoints of the line RT are R(-6, -5) and T(4, 0).
One point S has been given on line RT with the coordinates as(-2, -3)
Now we have to find the ratio between RS and ST.
Since distance between two points is measured by the formula
D =
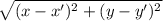
Where endpoints of the line are (x, y) and (x', y')
Now we plug in the values of points R and S in the formula to get the length of RS.
RS =
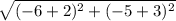
=
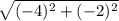
=

=
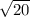
=
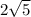 units
units
Now ST =

=

=
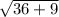
=

=
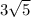
Now the ratio of RS and ST will be
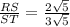
Or RS : ST = 2 : 3