Question

Assume that the number of watches produced every hour is normally distributed with a mean of 500 and a standard deviation of 100. what is the probability that in a randomly selected hour the number of watches produced is greater than 500

Answer 1

Answer: 0.5

Explanation:

Given : The number of watches produced every hour is normally distributed with a mean of 500 and a standard deviation of 100.

i.e.
`\mu = 500\text{ and } \sigma= 100`

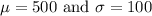
Let x be the number of watches produced every hour.

Then, the probability that in a randomly selected hour the number of watches produced is greater than 500 will be :

`P(x>500)=1-P(x\leq500)\\\\=1-P((x-\mu)/(\sigma)\leq(500-500)/(100))\\\\=1-P(z\leq0)\ \ [\because\ z=(x-\mu)/(\sigma)]\\\\=1-0.5\ \ [\text{ By z-table}]\\\\=1-0.5=0.5`

Hence, the probability that in a randomly selected hour the number of watches produced is greater than 500 =0.5.

Answer 2

To evaluate the probability that in a randomly selected hour the number of watches produced is greater than 500 we proceed as follows:
z=(x-μ)/σ
where:
x=500
μ=500
σ=100
thus
z=(500-500)/200=0

Thus:
P(x>500)=1-P(x<500)=1-P(z<0)=1-0.5=0.5

Answer: 0.5~50%