Question

The function f(x)=2^x and g(x)=f(x)+k.If k=-5,what can be concluded about the graph of g(x)?

the graph of g(x) is shifted horizontally
a.5 units to the left of the graph of f(x)
b. 5 units to the right of the graph of f(x)
c.the graph is not shifted horizontally from the graph of f(x)

Answer 1

Your answer will be choice C.. the value of 'k' will actually produce a vertical shift in the exponential function.

Answer 2

c. the graph is not shifted horizontally from the graph of f(x)

Explanation:

The parent function is given by
`f(x)=2^x`

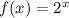
The transformation function is
`g(x)=f(x)+k`

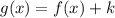
For k = -5, we have

`g(x)=f(x)-5\\\\g(x)=2^x-5`

The transformation of graph rule: Whenever, we add or subtract any constant in the function then there will be transformation in vertical direction.

• If we add a constant k to the function then the graph of the function will shift up by k units.

• If we subtract a constant k to the function then the graph of the function will shift down by k units.

Whenever, we add/subtract any constant in the x values then there would be transformation in horizontal direction.

Here 5 is subtracted in f(x) to get g(x) hence, here will be transformation in vertical direction not in horizontal direction.

Therefore, c is the correct option.

c. the graph is not shifted horizontally from the graph of f(x)