The park side length by the lake as given 180 meters.The walking path is in the shape of a rectangle with diagonal 200 square meters. Angles of a rectangle are 90 degrees.We have a right triangle with diagonal as the hypotenuse ,one of the leg as 180 meters and we need to find the adjacent side of the side by the lake that is the other leg
Pythagorean Theorem states: that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Or ,
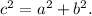 Where a,b are the legs of the triangle and c is the hypotenuse.
Where a,b are the legs of the triangle and c is the hypotenuse.
Substituting the values of c and a we have:
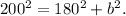
Or
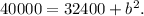
Subtracting 32400 both sides ,
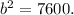
Or b= 87.17.= 87 m.
The side adjacent to the side by the lake is 87m.
Option A is the right answer.