Question

A weight attached to a spring is at its lowest point, 9 inches below equilibrium, at time t = 0 seconds. When the weight it released, it oscillates and returns to its original position at t = 3 seconds. Which of the following equations models the distance, d, of the weight from its equilibrium after t seconds?

a. d=-9cos(pi/3)t
b. d=-9cos(2pi/3)t
c. d=-3cos(pi/9)t
d. d=-3cos(2pi/9)t

Answer 1

Answer: B.

Explanation:

answer on edge

Answer 2

For a better understanding of the explanation provided here kindly go through the file attached.

Since, the weight attached is already at the lowest point at time, t=0, therefore, the equation will have a -9 as it's "amplitude" and it will be a Cosine function. This is because in cosine function, the function has the value of the amplitude at t=0.

Now, we know that the total angle in radians covered by a cosine in a given period is
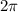`2\pi` and the period given in the question is t=3 seconds. Therefore, the angular velocity,
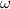`\omega` of the mentioned system will be:

`\omega=(2\pi)/(3)`

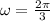
Combining all the above information, we see that the equation which models the distance, d, of the weight from its equilibrium after t seconds will be:

`d=-9cos((2\pi)/(3))t`

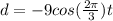
Thus, Option B is the correct option. The attached diagram is the graph of the option B and we can see clearly that at t=3, the weight indeed returns to it's original position.