The units of the quantity are:
![([kg] [m]^2)/([s]^2 [C])](https://img.qammunity.org/2019/formulas/mathematics/college/lr1hv9xinpj423sf9uezvl8st5n4o1tf6p.png)
We can isolate one
![([m])/([s]^2)](https://img.qammunity.org/2019/formulas/mathematics/college/88hq1qal7z15ln1zea5zspvm2qz4ystqln.png)
, which corresponds to an acceleration, a:
![= ([kg][m] a)/([C]) =](https://img.qammunity.org/2019/formulas/mathematics/college/o0qpct3eccxiaidr15pyyvrywyo59p2qc6.png)
[kg] corresponds to a mass, m; [m] corresponds to a length, L; C corresponds to a charge, Q:
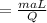
But the product ma is a force, F:
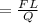
and the product FL is a work, so an energy, U:
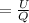
and this ratio corresponds to an electrical potential. So, the quantity is an electrical potential.