Question

A magnetic field of 0.55 g is directed straight down, perpendicular to the plane of a circular coil of wire that is made up of 550 turns and has a radius of 20 cm. 1) if the coil is stretched, in a time of 35 ms, to a radius of 50 cm, calculate the emf induced in the coil during the process.

Answer 1

The emf induced in the coil is given by Faraday-Neumann-Lenz law:

`\epsilon = - (\Delta \Phi)/(\Delta t)`
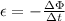
where

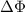
`\Delta \Phi` is the variation of magnetic flux through the coil

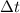
`\Delta t` is the time interval

The magnetic field intensity is

`B=0.55 G \cdot (1 \cdot 10^(-4) T/G) = 0.55 \cdot 10^(-4) T`

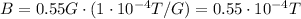
Since the magnetic field strength is constant, the variation of flux through the coil is given by

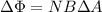
`\Delta \Phi = N B \Delta A` (1)
where N=550 is the number of turns, while
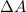
`\Delta A` is the variation of area of the coil. We can re-write (1) as

`\Delta \Phi = NB (\pi r_1^2 - \pi r_2^2)=(550)(0.55 \cdot 10^(-4) T)(\pi (0.20m)^2-\pi (0.50m)^2) =`

`=-0.020 Wb`

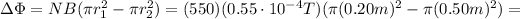
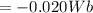
The time interval is
`\Delta t=35 ms=0.035 s`, therefore the induced emf is

`\epsilon = - (\delta \Phi)/(\Delta t)=- (-0.020 Wb)/(0.035 s)=0.57 V`