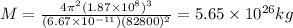Question

Saturn's moon Mimas has an orbital period of 82,800 s at a distance of 1.87x10^8m from Saturn. Using m central m= (4n^2d^3/GT^2) 1 determine Saturn's mass.

Determine Saturn's mass by rearranging Newton's version of Kepler's Third Law.

Answer 1

5.65×10^26kg here you go

Answer 2

`5.65* 10^(26) kg`

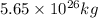
Step-by-step explanation:

From Kepler's third law: Mass of the planet is given by:

`M = (4\pi ^2d^3)/(GT^2)`

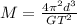
where, T is the time period of satellite revolving about the planet at a distance d. G is the gravitational constant = 6.67 × 10⁻¹¹ Nm²/kg²

Given, d = 1.87 × 10⁸ m

T = 82800 s

⇒
`M = (4\pi ^2 (1.87* 10^8)^3)/((6.67* 10^(-11))(82800)^2)=5.65* 10^(26) kg`