Question

Which polar coordinates represent the point plotted on the graph? Select all that apply. (2 answers)

a. (-4, 90 degrees)
b. (4, 90 degrees)
c. (4, -90 degrees)
d. (-4, 270 degrees)
e. (-4, -270 degrees)

Answer 1

1. A

2. B, D

3. A, D, E

4. C

5. A

Step-by-step explanation:

Answer 2

Answer: The correct options are (b) and (d).

Step-by-step explanation:

It the polar form
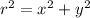`r^2=x^2+y^2`, where

`x=r\cos \theta,y=r\sin \theta`

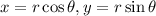
The polar coordinate are in the form of
`(r,\theta)`.

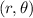From the given figure it is noticed that the value of r is 4 and
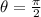`\theta=(\pi)/(2)` or
`90^(\circ)` .

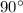So the point is defined as
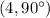`(4,90^(\circ))` and option b is correct.

The value,

`(r\cos \theta, r\sin \theta)=(0,4)`

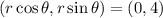
Check the each option if we get the same value then that option is correct.

For option a.

`(r\cos \theta, r\sin \theta)=(-4\cos 90^(\circ) , -4\sin 90^(\circ))=(0,-4)`

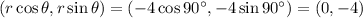
Therefore option (a) is incorrect.

For option c.

`(r\cos \theta, r\sin \theta)=(4\cos (-90)^(\circ) , 4\sin (-90)^(\circ))=(0,-4)`

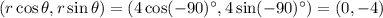
Therefore option (c) is incorrect.

For option d.

`(r\cos \theta, r\sin \theta)=(-4\cos (270)^(\circ) , -4\sin (270)^(\circ))\\(-4\cos (360-90)^(\circ) , -4\sin (360-90)^(\circ))=(0,4)`

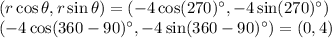
Therefore option (d) is correct.

For option (e).

`(r\cos \theta, r\sin \theta)=(-4\cos (-270)^(\circ) , -4\sin (-270)^(\circ))\\(-4\cos (270)^(\circ) , 4\sin (270)^(\circ))=(0,-4)`

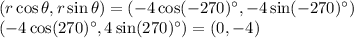
Therefore option (e) is incorrect.