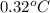Question

Calculate the freezing point of a 0.08500 m aqueous solution of nano3. the molal freezing-point-depression constant of water is 1.86°c/m. remember to include the value of i.

Answer 1

Answer : The freezing point of a solution is,
`0.32^oC`

Explanation :

First we have to calculate the Van't Hoff factor (i) for
`NaNO_3`.

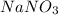The dissociation of
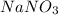`NaNO_3` will be,

`NaNO_3\rightarrow Na^++NO_3^-`

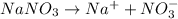
So, Van't Hoff factor = Number of solute particles =
`Na^++NO_3^-` = 1 + 1 = 2

Now we have to calculate the freezing point of a solution.

Formula used for lowering in freezing point :

`\Delta T_f=i* k_f* m`

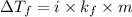
or,

`T_f^o-T_f=i* k_f* m`

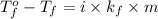
where,

`\Delta T_f` = change in freezing point

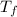`T_f` = temperature of solution = ?

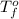`T^o_f` = temperature of pure water =
`0^oC`

`k_f` = freezing point constant =
`1.86^oC/m`

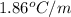
m = molality = 0.08500 m

i = Van't Hoff factor = 2

Now put all the given values in this formula, we get the freezing point of a solution.

`0^oC-T_f=2* (1.86^oC/m)* 0.08500m`

`T_f=0.32^oC`

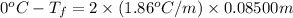
Therefore, the freezing point of a solution is,
`0.32^oC`

Answer 2

Depression in freezing point (Δ
`T_(f)`) =
`K_(f)`×m×i,
where,
`K_(f)` = cryoscopic constant =
`1.86^(0) C/m`,
m= molality of solution = 0.0085 m
i = van't Hoff factor = 2 (For
`NaNO_(3)`)

Thus, (Δ
`T_(f)`) = 1.86 X 0.0085 X 2 =
`0.03162^(0)C`

Now, (Δ
`T_(f)`) =
`T^(0)` - T
Here, T = freezing point of solution

`T^(0)` = freezing point of solvent =
`0^(0)C`
Thus, T =
`T^(0)` - (Δ
`T_(f)`) = -
`0.03162^(0)C`