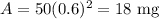Answer:
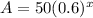
18 mg of medicine will be left in the patient's system after two hours.
Explanation:
Given,
The initial quantity of the medicine, P = 50 mg,
Also, it decreases every hour at a constant rate of 40%
That is, r = 40 %,
Thus, the quantity of the medicine after x hours,
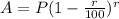
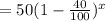
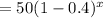
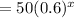
Which is the required exponential decay function that models this scenario.
The quantity of the medicine after 2 hours,