Question

he graph represents function 1, and the equation represents function 2: A coordinate plane graph is shown. A horizontal line is graphed passing through the y-axis at y = 6. Function 2 y = 2x + 7 How much more is the rate of change of function 2 than the rate of change of function 1? 1 2 3 4

Answer 1

2

Explanation:

I took the test

Answer 2

The answer is 2

Explanation:

Rate of change of function is given by :

`((f(x_(2))-f(x_(1))))/(x_(2)-x_(1))`

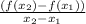
For function y = 6,

rate of change =

`=((f(x_(2))-f(x_(1))))/(x_(2)-x_(1))\\=(6-6)/(x_(2)-x_(1))\\=0`

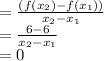
because the function is independent of x.

For function y = 2·x + 7,

rate of change =

`=((f(x_(2))-f(x_(1))))/(x_(2)-x_(1))\\=(2\cdot x_(2)+7-2\cdot x_(1)-7)/(x_(2)-x_(1))\\=(2\cdot x_(2)-2\cdot x_(1))/(x_(2)-x_(1))\\=(2\cdot (x_(2)-x_(1)))/(x_(2)-x_(1))\\=2`

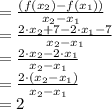
So, the rate of change of 2 is greater than rate of change of function 1 by 2 - 0 = 2.