Answer:
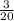 or
or
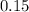
Explanation:
What is probability and how do we calculate it?
Probability, or the chances of a certain event happening at random, can be calculated with the following formula:
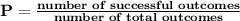
In the formula written above, the number of successful outcomes refers to how many times the desired event is achieved (in this case, how many ways an orange marble could be picked), and the number of total outcomes refers to how many events were possible (how many ways a marble could be picked). (Note that the term "events" can be thought of as similar to "ways" - 3 events in which an orange marble is picked simply means that there are 3 ways for orange marbles to be picked.)
How do we calculate probability in this scenario?
In this scenario, we have 3 orange marbles out of a total of 7 + 6 + 3 + 4 = 20 marbles in the pail, and we want to find the probability, or chances, that one randomly picked marble out of the total will be orange. Thus, the number of successful outcomes is how many different events will result in an orange marble being picked. This is equal to how many orange marbles there are, which is 3. Similarly, the number of total outcomes is equal to how many different events there can possibly be when picking. This is equal to the number of marbles (not necessarily orange) there are in the pail, which is 20.
From the above observations, we can conclude that the probability of a randomly drawn marble being orange is
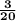 or
or
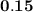 .
.