Question

During the first part of a​ trip, a canoeist travels 96 miles at a certain speed. the canoeist travels 15 miles on the second part of the trip at a speed 5 mph slower. the total time for the trip is 4 hrs. what was the speed on each part of the​ trip?

Answer 1

This problem is a problem using
d = r * t
First part of the trip
d = 96 miles
r = ??
t = ??

Second part of the trip
d = 15 miles
r = r - 5
t = 4 - t

Solve for r first.
96/r + 15/(r - 5) = 4 hours multiply through by r and r - 5
96(r - 5) + 15r = 4*(r - 5)(r) Remove the brackets on the left
96r - 480 + 15r = 4*r*(r - 5) Collect like terms on the left.
111r - 480 = 4r(r - 5) Remove the brackets on the right.
111r - 480 = 4r^2 - 20r Bring the left side over to the right side.
0 = 4r^2 - 20r - 111r + 480 Collect like terms.
0 = 4r^2 - 131r + 480

The only way I could do this was to use the quadratic equation.

`\text{x = }\frac{ -b \pm \sqrt{b^(2) - 4ac } }{2a}`

a = 4

b = - 131

c = 480

`\text{x = }\frac{ -(-131) \pm \sqrt{(-131)^(2) - 4*4*480 } }{2*4}`

`\text{x = }( 131 \pm √((17161) - 7680 ) )/(8)`

`\text{x = }( 131 \pm √(9481 ) )/(8)`

`\text{x = }( 131 \pm 97.37  )/(8)`

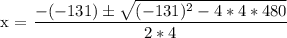
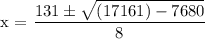
x = (131 + 97.38)/8
x = 28.55
x = (131 - 97.37)/8
x = 4.20

4.2 isn't going to work because the slower speed has to be larger than 5, otherwise you will get a negative speed (as this solution will give), so 4.20 is an extraneous solution.

r = 28.55 for the first part of the trip and
r = 23.55 for the second part of the trip.

Check.
Let's see if the times add up to 4
d/r = t
96/28.55 = 3.36
15/22.75 = 0.64

The times do = 4, so the rates are correct.

Answers
r1 = 28.55 for the 96 mile trip.
r2 = 23.55 for the 15 mile trip.