Question

Determine the domain of the function h(x)= 9x/x(x^2-36)

Answer 1

The function domain is:

`x<-6\quad \mathrm{or}\quad \:-6<x<0\quad \mathrm{or}\quad \:0<x<6\quad \mathrm{or}\quad \:x>6`

Explanation:

The domain of a function is the set of input or argument values for which the function is real and defined

Re-write the function as
`h(x)=(9x)/(x(x^(2)-6^(2)))`

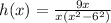
since, (a²-b²) =(a+b)(a-b)

`h(x)=(9x)/(x(x-6)(x+6))`

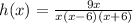
Find undefined singularity points x=0, x=-6, x=6

The function domain is:

`x<-6\quad \mathrm{or}\quad \:-6<x<0\quad \mathrm{or}\quad \:0<x<6\quad \mathrm{or}\quad \:x>6`

Answer 2

The function

`h(x)=(9x)/(x(x^(2)-36))`
is all real numbers except those that make the denominator zero.

The domain is "all real numbers except {-6, 0, +6}".