Question

A rubber ball dropped on a hard surface takes a sequence of bounces, each one 4/5 as high as the preceding one. If this ball is dropped from a height of 10 feet, what is the total vertical distance it has traveled at the time when it hits the surface for its fifth bounce?

A) 28 77/125 feet
B) 49 1/25 feet
C) 57 29/125 feet
D) 59 29/125 feet

Answer 1

The answer is 57 29/125 feet ⇒ answer (C)

Explanation:

∵ The ball dropped from a height 10 feet

∴ The vertical distance = 10 feet

∵ It bounces 4/5 as high as the preceding one

∴ 1st bounce = 10 × 4/5 = 8 (move down another 8)

∴ The vertical distance = 8 + 8 = 16 feet

∴ 2nd bounce = 8 × 4/5 = 6.4 (move down another 6.4)

∴ The vertical distance = 6.4 + 6.4 = 12.8 feet

∴ 3rd bounce = 6.4 × 4/5 = 5.12 (move down another 5.12)

∴ The vertical distance = 5.12 + 5.12 = 10.24 feet

∴ 4th bounce = 5.12 × 4/5 = 4.096 (move down another 4.096)

∴ The vertical distance = 4.096 + 4.096 = 8.192 feet

∵ The ball will hit the surface to make the 5th bounce

∴ The total vertical distance is :

10 + 16 + 12.8 + 10.24 + 8.192 = 57.232 = 57 29/125

Another way:

* We can use the formula of geometric sequence with

1st bounce distance (a) = 8 + 8 = 16 and ratio (r) = 4/5

and number of bounces (n) = 4 (hit the surface for its 5th bounce)

∵
`S_(n)=(a(1-(r^(n))))/(1-r)`

∴
`S_(4)=(16(1-((4)/(5))^(4)))/(1-(4)/(5))=47(29)/(125)`

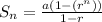
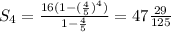
* Then we must to add the 10 feet

(the ball dropped from height 10 feet)

∴ The total vertical distance = 10 + 47 29/125 = 57 29/125 feet