Question

What is the expected value of the game if 3 hits pay​ $6, 2 hits pay​s $4, 1 hit pays $2, and 0 hits pay​s costs $4?

Answer 1

The probability of getting 3 hits is

`P\left(3\:hits\right)=0.7* 0.5* 0.3=0.105`

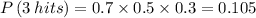
The probability of getting 2 hits is

`P\left(2\:hits\right)=\left(0.7* 0.5* 0.7\right)+\left(0.7* 0.5* 0.3\right)+\left(0.3* 0.5* 0.3\right)=0.395`

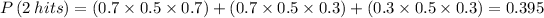
The probability of getting 1 hit is

`P\left(1\:hit\right)=\left(0.7* 0.5* 0.7\right)+\left(0.3* 0.5* 0.7\right)+\left(0.3* 0.5* 0.3\right)=0.395`

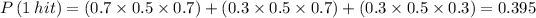
The probability of getting 0 hit is

`P\left(0\:hit\right)=0.3* 0.5* 0.7=0.105`

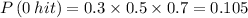
The expected value is solved by adding the products of the probability by the given pay. That is

`E=0.105\left(6\right)+0.395\left(4\right)+0.395\left(2\right)+0.105\left(4\right)=3.42`

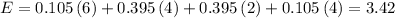
The expected value is $3.42.