Question

Complete the general solution to y=cos^-1(1) for K a whole number

Answer 1

I think that would be 0 +/- 360n  in degrees ans 0 +/- 0 + 2npi  in radians

Answer 2

If the equation is exactly the one you posted then the unique answer is:

`y = 0`

or what is the same:

`y=0K`

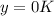
Step-by-step explanation:

If your equation is exactly the one you posted then it has only one solution: y = 0

Because the range of
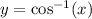`y=\cos^(-1)(x)` is the interval
`[0, \pi]`

The meaning of
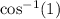`\cos^(-1)(1)` is to find the angle whose cosine is 1.

In the range of the function arccosine the only angle whose cosine is 1 is the angle 0.

But if your equation was the following one:

`\cos(y)=1`

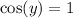
Then in that case we would have infinite solutions since it will be the set:

`y=\cos^(-1)(1)+2K\pi` where K is an integer, since the period of cosine is
`2\pi`

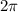
So, in such a case the solution set would be:

`y=0+2K\pi=2K\pi`

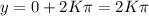
But for the equation you posted, the unique solution is: y = 0 or what is the same y = 0K