Question

Suppose the number of calls per hour to an answering service follows a poisson process with rate 4.

a.what is the probability that fewer than 2 calls came in the first hour?

Answer 1

With a mean of λ , the probability mass distribution (pmf) is given by

`P(k,\lambda)=\lambda^k*e^(-\lambda)/k!`

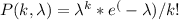
for &lambda; = 4, and k<2 (i.e. k=0 or 1)

P(k<2, &lambda; )=P(k=1, &lambda; ) + P(k=1, &lambda; )

`=4^0*e^(-4)/4!+4^1*e^(-4)/1!`

`=4^0*e^(-4)/4!+4^1*e^(-4)/1!`
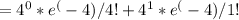
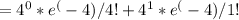
=0.01832+0.07326
=0.09158 (to the fifth place of decimal)

Note: Poisson processes have no memory, so 2 calls in first hour has the same probability as 2 calls in any other hour.