Question

1.

Find the amount of the annuity.

Amount of Each Deposit: $6,200

Deposited: Semiannually

Rate per Year: 6%

Number of Years: 5

Type of Annuity: Ordinary


$79,408.36

$81,720.90

$71,076.06

$73,208.36

Answer 1

To solve this we are going to use the future value of annuity ordinary formula:
`FV=P[ ((1+ (r)/(n) )^(kt) -1)/( (r)/(n) ) ]`
where

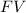
`FV` is the future value

`P` is the periodic payment

`r` is the interest rate in decimal form

`n` is the number of times the interest is compounded per year

`k` is the number of payments per year

`t` is the number of years

We know for our problem that
`P=6200` and
`t=5`. To convert the interest rate to decimal form, we are going to divide the rate by 100%:

`r= (6)/(100) =0.06`
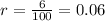
Since the deposit is made semiannually, it is made 2 times per year, so
`k=2`.
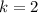
Since the type of the annuity is ordinary, payments are made at the end of each period, and we know that we have 2 periods, so
`n=2`.
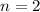
Lets replace the values in our formula:


`FV=P[ ((1+ (r)/(n) )^(kt) -1)/( (r)/(n) ) ]`

`FV=6200[ ((1+ (0.06)/(2) )^((2)(5)) -1)/( (0.06)/(2) ) ]`

`FV=71076.06`

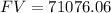We can conclude that the correct answer is $71,076.06