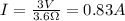Since the 3 lamps are connected in series, their equivalent resistance is equal to the sum of the three resistors:
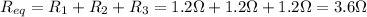
And the total current flowing in the circuit can be calculated by using Ohm's law:
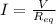
where V is the voltage of the battery. By using V=3 V, we find