Question

The equation of a parabola is 1/32 (y−2)2=x−1 .

What are the coordinates of the focus?


(1, 10)

(1, −6)

(−7, 2)

(9, 2)

Answer 1

The given equation of parabola is

`(1)/(32) (y-2)^2 = x-1`

Which can also be written as

`x = (1)/(32) (y-2)^2 +1`

Here vertex (h,k) is (1,2)

And value of a is

`a = (1)/(32)`

Formula of focus is

`(h+ (1)/(4a) , k)`

Substituting the values of h,k and a, we will get

`(1+ (1)/(4*(1/32) ) , 2} = (1+ 8,2) = (9,2)`

Therefore the correct option is the last option .

Answer 2

Answer: The correct option is (D) (9, 2).

Step-by-step explanation: We are given to find the co-ordinates of the focus for the following parabola:

`(1)/(32)(y-2)^2=x-1~~~~~~~~~~~~~~~~~~~~(i)`

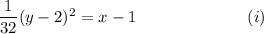
We know that the standard form equation of a parabola is

`(y-k)^2=4p(x-h),`

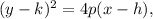
where the co-ordinates of the focus are (h+p, k).

From equation (i), we have

`(1)/(32)(y-2)^2=x-1\\\\\\\Rightarrow (y-2)^2=32(x-1)\\\\\Rightarrow (y-2)^2=4* 8(x-1).`

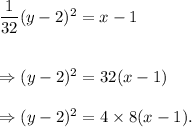
Comparing the above equation with the standard form equation of the parabola, we get

h = 1, k = 2, and p = 8.

Therefore, the co-ordinates of the focus are

`(h+p,k)=(1+8,2)=(9,2).`

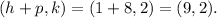
Thus, option (D) is CORRECT.