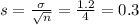Question

Yoonie is a personnel manager in a large corporation. each month she must review 16 of the employees. from past experience, she has found that the reviews take her approximately four hours each to do with a population standard deviation of 1.2 hours. let χ be the random variable representing the time it takes her to complete one review. assume χ is normally distributed. let 9 o be the random variable representing the mean time to complete the 16 reviews. assume that the 16 reviews represent a random set of reviews. 1. what is the mean, standard deviation, and sample size? 2. complete the distributions.

a. x ~ _____(_____,_____)
b. 9 o ~ _____(_____,_____)

Answer 1

Sample size is 16

Mean 4

Standard deviation of the sample is 0.3.

Step-by-step explanation

The Central Limit Theorem estabilishes that, for a random variable X, with mean
`\mu` and standard deviation
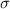`\sigma`, a large sample size can be approximated to a normal distribution with mean
`\mu` and standard deviation
`(\sigma)/(√(n))`.

In this problem, we have that:

The population has a mean of four hours, with a standard deviation of 1.2 hours. The sample is the 16 of the employees.

So

The sample size is 16, so
`n = 16`

The mean of the sample is the same as the population mean, so
`\mu = 4`.

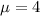The standard deviation of the sample is
`s = (\sigma)/(√(n)) = (1.2)/(4) = 0.3`