Question

Please help mee pleaseee​

Answer 1

`\qquad \qquad\huge \underline{\boxed{\sf Answer}}`

Here's the solution ~

Figure 1 :

Centre (A) = (0 , 0)

let's use distance formula to find the Radius (AB) :

`\qquad \sf \dashrightarrow \: \sqrt{(2- 0) {}^(2) + (0- 0) {}^(2) }`

`\qquad \sf \dashrightarrow \: \sqrt{(2) {}^(2) + 0}`

`\qquad \sf \dashrightarrow \: \sqrt{2 {}^(2) }`

`\qquad \sf \dashrightarrow \: 2`

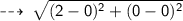
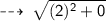
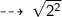
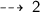
Radius = 2 units

Figure 2 :

Centre (A)= (2 , 1)

Let's solve for radius (AB) :

`\qquad \sf \dashrightarrow \: \sqrt{(2 - 2) { }^(2) + (3 - 1) {}^(2) }`

`\qquad \sf \dashrightarrow \: \sqrt{0 + (2) {}^(2) }`

`\qquad \sf \dashrightarrow \: \sqrt{2 {}^(2) }`

`\qquad \sf \dashrightarrow \: 2`

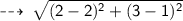
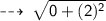
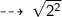
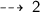
Radius = 2 units

Figure 3 :

Centre = (0 , -2)

now, let's find the Radius (AB) :

`\qquad \sf \dashrightarrow \: \sqrt{ ( - 3 - 0) {}^(2) + ( - 2 - ( - 2)) {}^(2) }`

`\qquad \sf \dashrightarrow \: \sqrt{( - 3) {}^(2) + 0}`

`\qquad \sf \dashrightarrow \: \sqrt{( - 3) {}^(2) }`

`\qquad \sf \dashrightarrow \: √(9)`

`\qquad \sf \dashrightarrow \: 3`

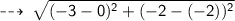
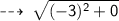
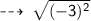
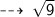
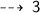
Radius = 3 units

Answer 2

• See below

Explanation:

Determine the center by coordinates (x, y) of point A.

Determine the radius by the difference of respective coordinates of the A and B points (the center and the point on the circle).

#1

Points given:

• A = (0, 0) and B = (2, 0)

• The center is (0, 0)
• The radius is 2 - 0 = 2 units (the distance between two horizontal points)

#2

Points given:

• A = (2, 1) and B = (2, 3)

• The center is (2, 1)
• The radius is 3 - 1 = 2 units (the distance between two vertical points)

#3

Points given:

• A = (0, -2) and B = (-3, -2)

• The center is (0, -2)
• The radius is 0 - (-3) = 3 units (the distance between two horizontal points)