Question

Which polynomial function has a leading coefficient of 1, roots –3 and 8 with multiplicity 1, and root 4 with multiplicity 2?

f(x) = 2(x + 3)(x + 4)(x – 3)
f(x) = 2(x – 8)(x – 4)(x + 3)
f(x) = (x + 8)(x + 4)(x + 4)(x – 3)
f(x) = (x – 8)(x – 4)(x – 4)(x + 3)

Answer 1

f(x) = (x-8)(x-4)(x-4)(x+3)

Answer 2

f(x) = (x – 8)(x – 4)(x – 4)(x + 3)

Explanation:

A polynomial function with roots
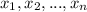`x_(1), x_(2), ..., x_(n)` has the following format:

`f(x) = a(x - x_(1))(x - x_(2))...(x - x_(n))`

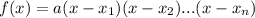
In which a is the leading coefficient.

In this problem, we have that:

Leading coefficient 1, so
`a = 1`

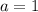
roots -3 and 8 with multiplicity 1, so
`(x + 3)(x - 8)`.

root 4 with multiplicity 2, so
`(x - 4)^(2) = (x - 4)(x - 4)`

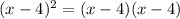
So the correct answer is:

f(x) = (x – 8)(x – 4)(x – 4)(x + 3)